SBRT: Progress in Pancreatic Cancer!
The push towards higher doses and maybe a new radiation protector
Great study. Bittersweet timing.
A new study was just released - just days after the unexpected passing of the lead author - Cullen Taniguchi. He was a brilliant scientist in both his laboratory work and in the clinic. He touched the lives of so many in our field and his legacy will live on in his work and in those who he impacted. Today, we’ll look at one piece of his recent work in pancreatic cancer.
First off, it is yet ANOTHER site where we are making strides in using radiation where, back when I trained, we didn’t push dose and really didn’t cure anyone. At MD Anderson back in the late 90’s the most common dose was 30 Gy in 10. Sometimes more protracted to 4500 or 5000 cGy but often, we did it shorter / quicker. This trial, in contrast, looked at treating borderline resectable or locally advanced pancreatic cancer with SBRT giving doses we thought were not possible in that region of the body just a few years ago.
It is a Phase I/II trial and SBRT doses were 50 Gy, 55 Gy, and 60 Gy in five fractions - adaptively assigned in real time using Bayesian estimates.
Further there was a second basic laboratory question added in - again major kudos to the designers of this clinical / laboratory approach. The second piece / question to the trial was to add avasopasem or placebo IV prior to treatment (within 180 min). The concept is avasopasem is potential radioprotector. The primary objective of the study was to find the optimal dose of SBRT with avasopasem or placebo as determined by the late onset EffTox Method (a balance of efficacy and toxicity to guide recommendations).
In summary, its a rather complex design looking to see if 1) avasopasem can help reduce toxicity and 2) determine the ideal dose with and without this extra medication. It uses Bayesian approaches to help streamline and maximize the effort.
Bayesian Statistics:
Link to Statistical Thinking - a great general statistics resource.
I want to touch upon this aspect of the trial for a few reasons. First, I think it was one reason why people seem to often dismiss / discount the Esophageal randomized data discussed here:
It showed that protons had much less total toxicity than a photon approach, especially for those who went on to have curative surgery. (The second issue was the use of a total toxicity burden approach and the third, in my opinion, was the approach of the write up / presentation).
What is new and unfamiliar is often a reason to dismiss. Many are busy and don’t have the ability or time to go read for a week and learn a new approach to statistics. It is far easier to simply say something dismissive like “they knew the only way to win was to make up all this extra complexity” and simply move along.
But a Bayesian approach is really a great math tool that we can utilize to help us more rapidly answer questions in our specialty. And here, really smart people are demonstrating that approach. A small cohort of patients (only 42) are being used to fine tune dose and drug recommendations. Slowly this approach is gaining traction and so, we’ll quickly review some basics.
The broad basics of a Bayesian approach:
A bit of history: Bayesian statistics is named after Thomas Bayes, an 18th-century mathematician. So the math has been around for quite a while. It is not some new super complex fancy approach - just less often utilized.
In traditional (frequentist) statistics, probability is often interpreted as the long-term relative frequency of an event occurring based on repeated, hypothetical experiments. For example, if you were to toss a fair coin many times, the probability of getting heads is interpreted as the limit of the ratio of the number of times heads occurs to the total number of tosses as the number of tosses approaches infinity.
We all should know this example. The story goes, you are in a saloon in the old west and you sit down and guy asks you to call heads or tails. At what point in the upcoming loosing streak are you suspicious that you are being cheated? Most get quite convinced around flip 4 or 5.
And the math goes like this. Odds of heads landing twice is 1/2 x 1/2. 25%. Flip it again - 12.5%. And again - 6.25%. And again - 3.125%. And at somewhere between flip 4 and flip 5, we magically “decide” the coin is rigged - a p-value of 0.05. That “statistically something is wrong”, i.e., I’m being cheated.
Nearly every decision in medicine is based on this arbitrary decision point. Today, we now often add “confidence intervals” which are based on normal distributions (another large assumption) to “help” with our decision making. But a central premise is, we gain no knowledge “during” the process. And in today’s world, pharma understands that with enough trials and enough secondary endpoints, one is nearly guaranteed to find success. If you doubt this, spend 20 minutes flipping a coin and you too will find an instance where you are certain it is “not a fair coin” if a small segment of flips is taken out of the broader context of your other attempts.
On the other hand, Bayesian statistics takes a different approach to probability. Instead of considering probability as a long-term frequency, it interprets probability as a measure of belief or confidence in a particular event or hypothesis. In this Bayesian framework, probability is subjective and reflects an individual's or a system's degree of belief in the likelihood of an event.
So, in Bayesian statistics, you start with an initial belief about a hypothesis, called the prior probability. As new data becomes available, you update this belief using Bayes' theorem, which combines the prior probability with the likelihood of the observed data given the hypothesis to calculate a posterior probability. This posterior probability then becomes the updated belief or certainty about the hypothesis in light of the new evidence.
In essence, Bayesian statistics provides a framework for updating beliefs based on both prior knowledge and the observation of data.
Bayesian statistics is particularly useful in situations with limited data, allowing for the incorporation of prior knowledge and updating beliefs as new evidence becomes available.
Here’s a look at key definitions and the “theorem” for completeness:
Prior Probability: This is the initial belief or probability assigned to a hypothesis before considering new evidence. It reflects what is known or believed based on existing information.
Likelihood: This represents the probability of observing the data given a particular hypothesis. It describes how well the hypothesis explains the observed data.
Posterior Probability: This is the updated probability of a hypothesis after taking into account the observed data. It combines the prior probability and the likelihood of the data.
Bayes' Theorem: The core mathematical formula in Bayesian statistics is Bayes' theorem, which relates the prior probability, likelihood, and posterior probability. It helps update beliefs based on new evidence.
Mathematically, Bayes' theorem is expressed as:
P(A∣B)=P(B∣A)⋅P(A) / P(B)
Where:
P(A∣B) is the posterior probability of hypothesis A given evidence B.
P(B∣A) is the likelihood of observing evidence B given hypothesis A.
P(A) is the prior probability of hypothesis A.
P(B) is the probability of observing evidence B.
Enough math, but understand that as a small field with limited resources, we must be really efficient to compete in the marketplace. Kudos to the authors for their approach and creativity to move forward - again, they are running the trial with 42 patients looking to answer 2 different questions. That is the power of this approach.
Avasopasem
If you are a bit older, you’ll remember Amiphostine. Back in the day, there was some pretty good data for this older drug helping to limit toxicity in head and neck cancer patients. It was given via an IV within an hour or so of treatment and then just following the infusion, the radiation was given.
My clinical experience was that, while it may have helped for some, it actually amplified the toxicity profile of treatment for a pretty big cohort of those patients. It’s probably been 15 years since I’ve used it in the clinic - days long passed.
But it was labeled as a “free radical scavenger”.
And Avasopasem is something similar - “a small molecule redox active manganese containing superoxide dismutase mimetic - GC4419”.
Here is a quite pertinent link in you are more interested - a recent rejection of the drug by the FDA in head an neck cancer - for mucositis.
FDA Rejects NDA for Avasopasem in RT-Induced Severe Oral Mucositis
I’m not a basic lab guy, but today, I file it next to amiphostine. Maybe it is much better or maybe not. I’m not sure that the mechanism of actions are exactly similar on a cellular level, but in the big picture, I think they are reasonable approximations. (As always, please comment below if this is not a reasonable comparison.)\
But at least now you have a feel for two of the main “complexities” in the trial. The rest, pancreatic cancer, SBRT and dosing, are hopefully much more known.
THE TRIAL FINDINGS:
A few details on the approach.
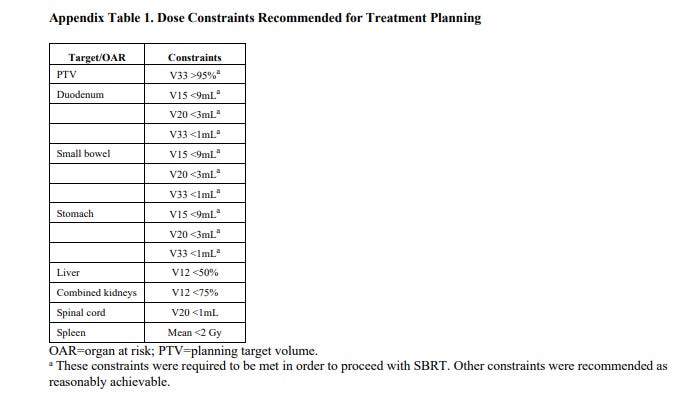
The planning target volume was constructed by adding the internal gross tumour volume and tumour-vessel interface and doing a 3 mm radial expansion. This planning target volume was prescribed to 33 Gy in five fractions with a simultaneous integrated boost to the trial-prescribed dose (50 or 55 Gy in five fractions) as long as dose constraints for critical organs at risk (eg, the stomach, duodenum, or small bowel) were met. No elective nodal irradiation was done.
We’re seeing this more and more - just like in PACE-B - there is a PTV dose that is markedly less than the headline CTV dose. I like the approach but it speaks to the nuance in many of these SBRT trials and how you should not attempt to read and implement these approaches without some real due diligence on your behalf.
Any and all of these approaches are closer to the razors edge of benefit / high toxicity risk.
Did the Avasopasem shift the outcomes?
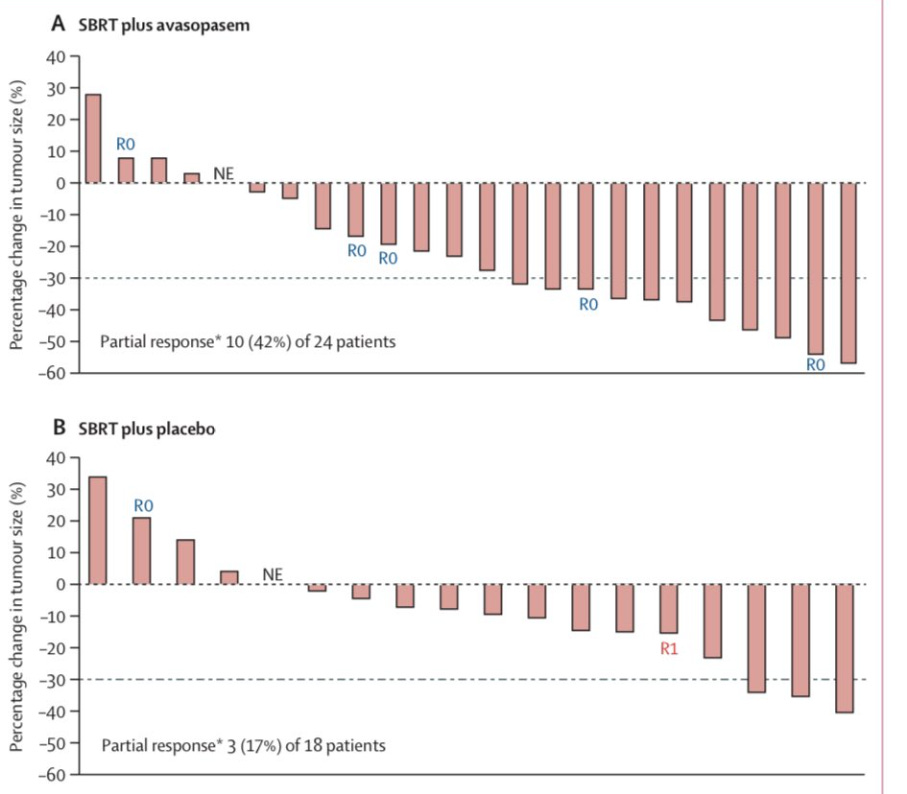
The answer appears to be - perhaps. Certainly all the trends are in the correct direction with respect to response and clinical outcomes. Overall survival, Progression free survival, local regional control, and disease progression all favor the addition of the drug. But notice, these are response changes, not toxicity improvements.
And below we see this differently. The graph below shows response to treatment. There is a slight shift towards more patients having a partial response (the number of patients reaching “below” the dashed line).
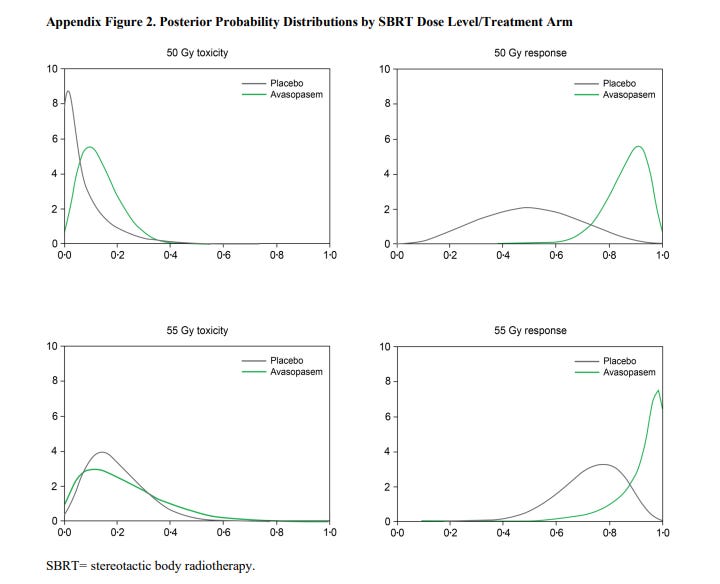
From the appendix, I think this is actually easier to see - a Bayesian illustration of posterior probabilities.
As shown below, there are some changes on both toxicity and response - with actually the response aspect being a more dramatic shift. (ie, the curves are “more different” in appearance for response than they are for toxicity)
Ultimately the statistical model recommended the addition of avasopasem with dosing to be 50 Gy or 55 Gy. Still, I’m a little cautious on the drug based on this small series. Above you can see that the toxicity difference actually appears less dramatic than the response data and if you look at higher grade toxicity, you see this:
Serious adverse events of any cause were reported in three (17%) of 18 patients in the placebo group and six (25%) of 24 in the avasopasem group
In the end, this is an interesting trial. The work is progressing along to further investigation. Avasopasem is now being evaluated in this Phase 2b study looking at SBRT with or without this drug for pancreatic cancer.
Phase 2b Study of GC4711 in Combination With SBRT for Nonmetastatic Pancreatic Cancer
In Closing:
Once again, SBRT is allowing us to push more dose into place that we did not think possible just a few years ago. We are demonstrating progress against a number of tumors using this approach:
Consider the following sites for SBRT with strong new positive data:
And now: pancreatic cancer. These are just the ones I’ve covered in the past quarter on this Substack. Six separate articles on strengthening data in 6 sites.
Will the drug be a homerun addition that allows us to shift the risk / benefit profile of treatment? There I’m less clear, but I love the integration of a basic science approach and the use of robust statistical modern approach to allow us - a small field - an opportunity to compete on the playing field where we are outspent 100:1.
Kudos to the entire team for an outstanding contribution as we all keep pushing for better outcomes for our patients!
To keep up to date, subscribe or if you got here, consider hitting the like button. Little things help. Thanks for wonderful support.






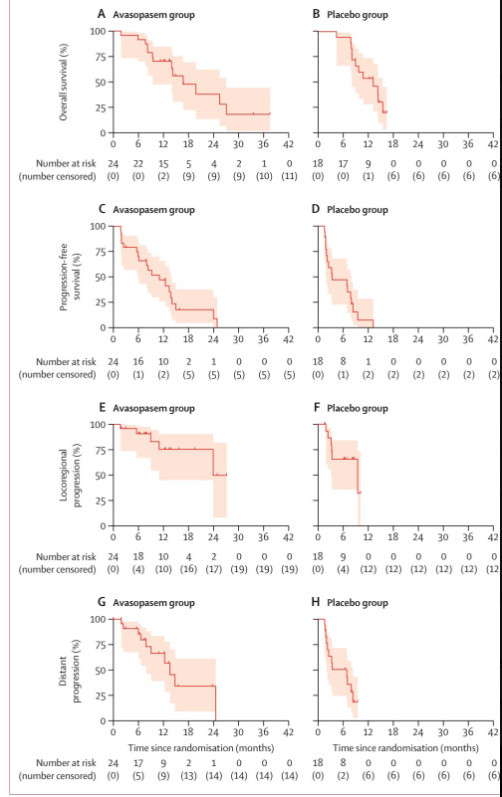
Unfortunately the subsequent 2b trial was closed after an interim analysis. That being said the survival with this dosing schema of sbrt are excellent compared to historical outcomes, which hopefully continues to build the role for rt in this tough disease using our best technology.